Understanding 5 Hundreds 10: A Step-by-Step Guide!

Can a seemingly simple mathematical expression unlock a deeper understanding of numerical relationships? The answer is a resounding yes, as exploring "5 hundreds 10" unveils the fundamental principles of place value and the power of multiplication.

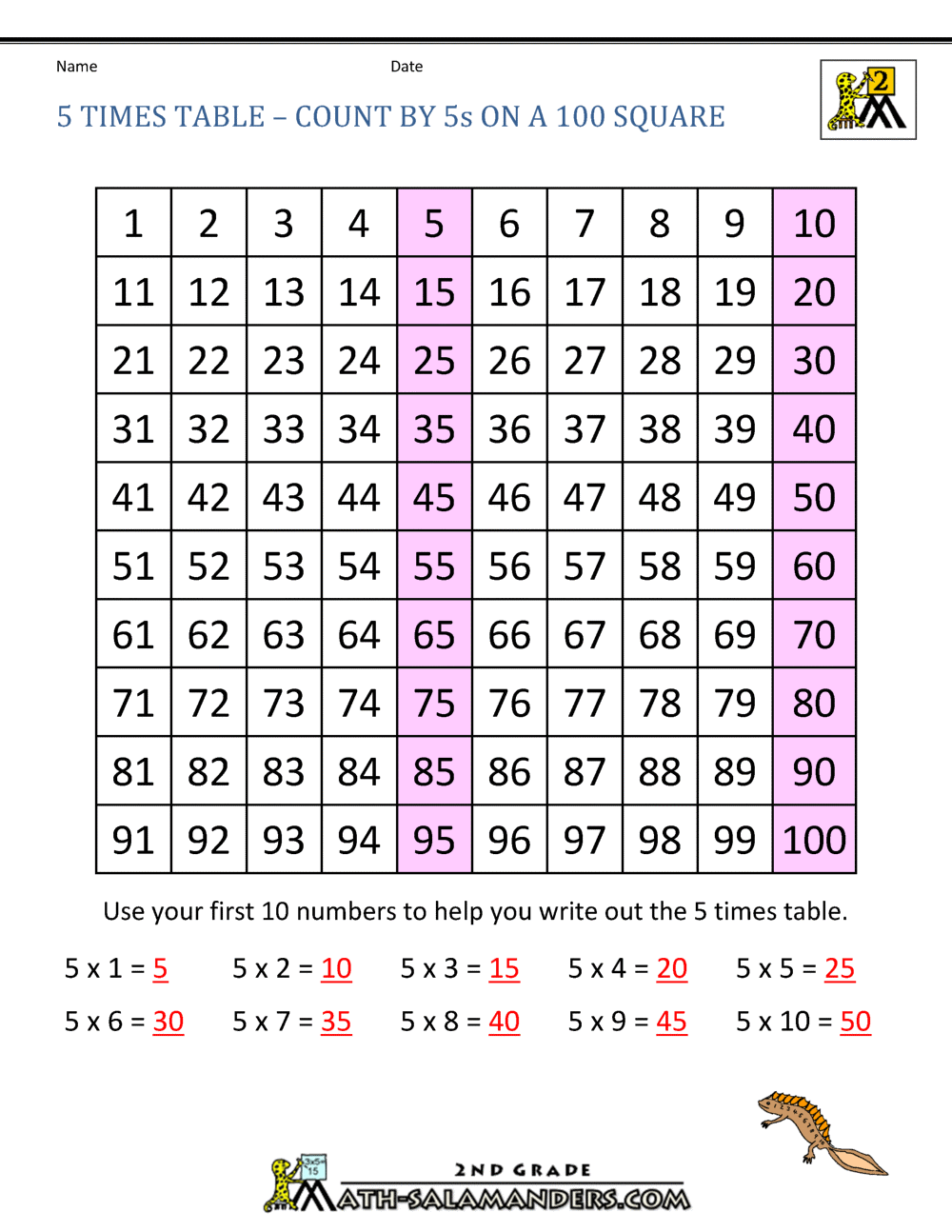
To delve into the core of this question, we begin by deconstructing the phrase "5 hundreds." In numerical terms, this represents a straightforward multiplication: 5 multiplied by 100, which equals 500. This initial step highlights the significance of understanding place value the foundation upon which our number system is built. The word "hundreds" immediately tells us we're dealing with a quantity that is a multiple of 100. The placement of the digit 5 within the number 500 is crucial; it signifies five groups of one hundred.

Next, we apply the second part of the equation, multiplying the calculated value by 10. This yields 500 10 = 5000. Thus, the solution to "5 hundreds 10" is 5000. This outcome demonstrates how a seemingly simple operation can escalate the magnitude of a number significantly.

• Simple Robbery Definition Examples And Legal Nuances Explained
• Nancy Drew Quotes Unforgettable Lines Adventures

Let's consider another numerical example, the number 4553. This number provides a useful framework for grasping the nuances of place value. The digit 5 in the hundreds place has a value of 500. However, the 5 in the tens place represents only 50. The discrepancy between these two values offers an opportunity to explore a fascinating relationship. We can determine how many times larger the 5 in the hundreds place is than the 5 in the tens place by dividing 500 by 50. The result is 10. Therefore, the 5 in the hundreds place is 10 times greater than the 5 in the tens place.

The process of converting the expression "5 hundreds times 10" into unit form further solidifies our comprehension. The phrase "5 hundreds" is equivalent to the number 500, which results from multiplying 5 by 100. This step reiterates the definition of "hundreds" as referring to the number 100. Therefore, the mathematical representation of "5 hundreds" is 5 100 = 500. The subsequent multiplication by 10 leads us to 500 10 = 5000. Multiplication, often signified by the cross symbol (), a point (), or juxtaposition, is one of the four fundamental arithmetic operations.

Now, consider the conversion of a number into scientific notation. A number written in scientific notation takes the form of a 10^b and is read as "a times 10 to the power of b." The key here is that we need to move the decimal point to a location to get "a" value. Trailing zeros are only removed if they appear to the left of the decimal point. Consider the number 459,608. To convert this into scientific notation, we move the decimal 5 places to the left, resulting in 4.59608. Since we moved the decimal to the left, the value of 'b' is positive. This method is particularly useful for representing exceedingly large or small numbers in a more manageable form.

• Obliterated Nude Scenes Sex Scenes See Them Now
• Uncover The Sensual World Fifty Shades Trilogy Deals Reviews

Let's evaluate the expression: "(5 hundreds 5 tens) 10." This question is rooted in place value understanding. In standard form, "5 hundreds 5 tens" is written as 550. To compute the final result, we perform the multiplication: 550 10 = 5,500.

The term "number" refers to an arithmetical value expressed by a word, symbol, or figure that represents a specific quantity used for counting and calculations. Therefore, when we address the question of writing "5 hundreds times 10" in unit form, we are essentially determining the numerical value of the expression.

Let's break down the term "5 hundreds" again. As 1 hundred equals 100, 5 hundreds can be expressed as 5 100. Which yields 500. Now we have to multiply 500 by 10. This calculation leads us to the final answer: 500 10 = 5000.

Consider the expression: "(6 ten thousands + 5 hundreds) 10." To address this, we need to first understand what '6 ten thousands' and '5 hundreds' represent in numerical terms. Converting the words to numbers, we have: 6 ten thousands = 6 10,000 = 60,000; and 5 hundreds = 5 100 = 500. The sum of these two values is 60,000 + 500 = 60,500. This concept underscores the importance of comprehending the different place values and performing the additions correctly to reach the correct final answer.

Multiplication can also be understood as repeated addition. For instance, the multiplication of 3 times 4 equals 12, which is the same as adding 4 three times (4 + 4 + 4 = 12). Each place value is a multiple of ten greater than the position to its right. For instance, consider a number like 4,349,394.382. We have 4 millions, 3 hundred thousands, 4 ten thousands, 9 thousands, 3 hundreds, 9 tens, 4 ones, 3 tenths, and 8 hundredths, and 2 thousandths, we can see how to read the number aloud.

Let's elaborate on place value. When we multiply ten by 4 ten thousands, we get 40 ten thousands, which is the same as 4 hundred thousands. 10 4 ten thousands = 40 ten thousands = 4 hundred thousands.

Now let us explore some fundamental mathematical equations. We have to fill in the blanks to make the following equations true:

• 10 times 4 ones = 40 ones = 40
• 10 times 2 tens = 20 tens = 200
• 5 hundreds times 10 = 50 hundreds = 5000

We can also delve into the relationship between numbers and their place values. For instance, in the context of "5 hundreds times 10," since 1 hundred equals 100, 5 hundreds is the same as 5 100. Therefore, we have (5 100) 10 = 5000. The final expression: 5 hundred times 10 unit in standard form is 5000.

Let's delve into the structure of place value with some examples. 10 times 6 hundreds is 60 hundreds, which equals 6 thousands. Similarly, 10 times 8 hundreds yields 8 thousands. The value of 40 hundreds is equivalent to 4 thousands.

To clarify, the following equations can be solved as follows:

• (a) 10 times 4 ones = 10 4 ones = 40
• (b) 10 times 2 tens = 2 tens = 200
• (c) 5 times hundred times 10 = 50 hundreds = 5000

Another way to look at this is: 10 times as many as 1 hundred is 10 100, which is 10 hundreds, or 1000.

Consider the simple equation: 8 10,000 = 80,000. And another one: 5 hundreds times 10 unit, first convert 5 hundreds to a number. This is 5 100 = 500. Combine these values by adding them: 80,000 + 500 = 80,500. Then, multiply the result by 10: 80,500 10 = 805,000.

In standard form, the solution to (7 ten thousand 5 hundreds) x 10 is 705,000. In standard form, the answer is:

This all is a detailed explanation of how to address the question of 5 hundreds 10, providing clarity on how to approach similar arithmetic problems.

Detail Author:

• Name : Dr. Retha Krajcik II
• Username : nathanael85
• Email : kbartoletti@yahoo.com
• Birthdate : 1971-11-15
• Address : 899 Labadie Junction Apt. 871 Aldamouth, CO 56070
• Phone : +14709341315
• Company : Orn-Breitenberg
• Job : Molder
• Bio : Officia voluptate autem accusantium quidem optio. Voluptate dignissimos eligendi soluta eos est.

Socials

twitter:

• url : https://twitter.com/garrett.romaguera
• username : garrett.romaguera
• bio : Velit fugit cumque temporibus ea error dolor tempore. Nesciunt dolorem quia autem nulla quia.
• followers : 3847
• following : 1760

instagram:

• url : https://instagram.com/garrett_romaguera
• username : garrett_romaguera
• bio : Sed numquam maiores voluptatum ea ducimus. Sunt autem rerum dolor quis. Dolor maiores ab ut qui.
• followers : 3364
• following : 823

linkedin:

• url : https://linkedin.com/in/garrettromaguera
• username : garrettromaguera
• bio : Error architecto neque consequatur itaque.
• followers : 2258
• following : 169

facebook:

• url : https://facebook.com/gromaguera
• username : gromaguera
• bio : Iure molestiae nostrum nobis nesciunt mollitia in minus.
• followers : 3430
• following : 947