Understanding Standard Form Of Equations: A Comprehensive Guide
Can the seemingly simple act of writing an equation drastically alter our approach to problem-solving? The answer, surprisingly, is a resounding yes, and it all hinges on understanding and skillfully employing the concept of "standard form."
We're all familiar with equations; they're the backbone of mathematics, the language in which we describe relationships between numbers, variables, and concepts. But did you know that equations can be presented in different "dialects," each offering unique advantages depending on the task at hand? Among these, slope-intercept form and standard form are two of the most commonly used and important. This article will focus on understanding standard form, its nuances, and how it can revolutionize your approach to solving equations, especially in more complex scenarios.
| Aspect | Details |
|---|---|
| Definition of Standard Form for Linear Equations | Ax + By = C, where A, B, and C are real numbers, and A and B are not both zero. |
| Purpose | To provide a consistent and organized structure for representing linear equations, simplifying various mathematical operations. |
| Key Features |
|
| Advantages |
|
| Disadvantages |
|
| Applications |
|
| Example | 2x + 3y = 6. In this case, A = 2, B = 3, and C = 6. This can be easily translated into slope-intercept form or utilized directly. |
| Transforming from Slope-Intercept Form (y = mx + b) | To convert, rearrange the equation so that the x and y terms are on one side and the constant is on the other. Example: y = 2x + 3 becomes -2x + y = 3 (or, multiplying by -1, 2x - y = -3). |
| Working with Systems of Equations | Standard form helps in aligning variables when solving by elimination. For example:
|
| Finding Intercepts |
|
| Note on Coefficients | While not always required, it's common practice to express the coefficients (A, B, and C) as integers and ensure the leading coefficient (A) is positive. |
| Standard Form for Quadratic Equations | The form is ax + bx + c = 0, where a, b, and c are constants, and a 0. |
| Converting to Vertex Form | Complete the square or find the vertex to convert the equation to the vertex form, which provides insights into the parabola's turning point. |
| Standard Form for Numbers (Scientific Notation) | Used for very large or small numbers, it is expressed as a x 10^b, where 1 a < 10, and b is an integer. |
| Reference | Mathsisfun.com |
Standard form is particularly valuable when dealing with systems of equations. Let's illustrate this with a simple example. Imagine we are given a system of equations, like this:
- Port Huron Mi History Maps Facts Your Guide To The Blue Water Area
- Find Suzanne Rosenberg Info Profiles Contact More
- 2x + y = 5
- x - y = 1
These equations are already in standard form, which makes using the elimination method exceptionally straightforward. By simply adding the two equations together, the 'y' terms cancel out, allowing us to solve for 'x' immediately.
The standard form, also known as the general form, of a linear equation represents one of the fundamental ways to articulate linear equations. In the domain of linear equations with two variables, standard form adopts the structure: Ax + By = C, where A, B, and C are recognized as real numbers, and it's imperative that both A and B are not simultaneously zero. This structure presents a clear and organized method for representing equations, which is particularly advantageous when we want to solve systems of linear equations. By arranging the equations in this manner, the coefficients of like variables are conveniently aligned, which greatly eases the process of eliminating a variable through addition or subtractiona cornerstone technique in solving systems of equations.
The standard form of a linear equation in one variable takes a slightly different shape, presented as Ax + B = 0. This format is useful for solving single-variable equations and sets the stage for grasping the more complex two-variable structure. The importance of the standard form extends beyond merely solving equations; it aids in graphing linear equations. By setting x or y to zero, we can easily determine the x-intercept and y-intercept, key points for plotting the line on a graph. It is important to remember that equations aren't always presented in their standard form; a fundamental skill is to rearrange an equation into this form to fully unlock its utility.
- Verizons Craig Silliman New Role Compensation Details Latest News
- Damian Payne Career Family Tributes Latest Updates
To get an equation into standard form, follow these steps. First, isolate the constant (the term with no variable) on the right side of the equation by adding and subtracting terms from both sides. Then, if necessary, manipulate the equation so that the coefficient of 'x' is positive. Finally, confirm that all coefficients are integers for optimal clarity. The ultimate goal is to transform any linear equation into the precise format of Ax + By = C.
The standard form of a line is a special way of writing the equation of a line. This form is another way to write the equation, which is defined as Ax + By = C, where A, B, and C are real numbers, and A and B are both not zero. This definition is critical, as it sets the groundwork for all subsequent applications of the standard form. Think of it as the agreed-upon, organized way of displaying these linear relationships.
Consider the standard form of a quadratic equation: ax + bx + c = 0. In this context, a, b, and c are known values, while x represents the variable, the unknown we aim to solve for. This form, although fundamental, is not the only way quadratics are expressed. Its essential to recognize that while ax + bx + c = 0 is standard, other forms such as vertex form (which reveals the vertex of the parabola) are also vital tools in analyzing quadratic functions. Learning to convert between these forms allows for a comprehensive understanding of the quadratic equation's behavior.
Finding the slope and y-intercept from a standard form equation isn't immediately obvious, unlike the slope-intercept form (y = mx + b). One way to find the slope is to rearrange the equation into slope-intercept form. For example, starting with 2x + 3y = 6, we can subtract 2x from both sides to get 3y = -2x + 6, and then divide everything by 3 to arrive at y = -x + 2. The slope is - and the y-intercept is 2. Alternatively, the slope can be calculated directly from the standard form using the formula: -A/B. The y-intercept is found by setting x=0 in the standard form equation and solving for y, which becomes C/B.
Let's consider an exercise to demonstrate the conversion and manipulation of equations in standard form. Write two equations in standard form that are equivalent to x - 2y = 3. To write one equivalent equation, you can multiply both sides of the original equation by a constant (other than zero). For example, multiplying the original equation by 2 gives us 2x - 4y = 6. For another equivalent equation, you could multiply the equation by -1, resulting in -x + 2y = -3. This demonstrates that standard form is not unique; there are many equivalent ways to represent the same line.
Now, lets write an equation in standard form of the line through (3, 1) and (2, -3). First, calculate the slope (m): m = (-3 - 1) / (2 - 3) = -4 / -1 = 4. Then, using the point-slope form (y - y1 = m(x - x1)), substitute the values: y - 1 = 4(x - 3). Simplify this to y - 1 = 4x - 12. Finally, rewrite in standard form: -4x + y = -11 or 4x - y = 11. This shows how to move from a problem statement (two points) to a standard form equation.
Let's look at an example. Write two equivalent equations in standard form for 2x - 6y = 4. To create one equivalent equation, multiply all the terms by 2, resulting in 4x - 12y = 8. To form another, we could divide all the terms by 2: x - 3y = 2. These different forms all represent the same line, emphasizing the flexibility of standard form.
The standard form of linear equations is one of the many ways in which a linear equation is expressed. Expressed as Ax + By = C, where A, B, and C are integers, and x and y are variables, it represents the general form of a linear equation that has two variables. This form is the most frequently accepted form of an equation and is a common form to use when graphing or solving. For polynomials, standard form requires that the terms be written in descending order of their degree. It's a crucial element of order in mathematics, enabling clarity and consistency.
Standard form is a method for writing linear equations in the format Ax + By = C. The main purpose of standard form is to make certain mathematical operations, such as solving systems of equations, easier. The standard form of a quadratic equation looks like this: ax + bx + c = 0. It is the framework on which much algebraic understanding is built.
When we consider how standard form aids in visualizing and solving equations, we realize its pivotal role. So, to rewrite an equation in standard form, move the x and y terms to the same side of the equal sign. If necessary, multiply or divide both sides by a constant to eliminate fractions or decimals and ensure that the coefficients are integers. Make sure 'A' is positive, and the equation is now in its standard form, ready for use in various mathematical tasks.
Equations can be both easy and difficult to solve, depending on their size, elements, and operations. For better understanding, we can divide equations into two types: linear and non-linear. Standard form is essential for both, offering a straightforward structure. Understanding standard form opens a path toward grasping the broader mathematical landscape.
The standard form is also known as the general form of a linear equation, which is just one of three ways we can express linear equations. The other two are slope-intercept form and point-slope form. However, standard form is uniquely suited to certain types of algebraic manipulations and, importantly, is crucial for solving systems of equations via elimination. The standard form formula represents the frequently accepted format of an equation, which is a common form of an equation. It is expressed as Ax + By = C, where A, B, and C are integers, and x and y are variables. This general form of a linear equation has two variables.

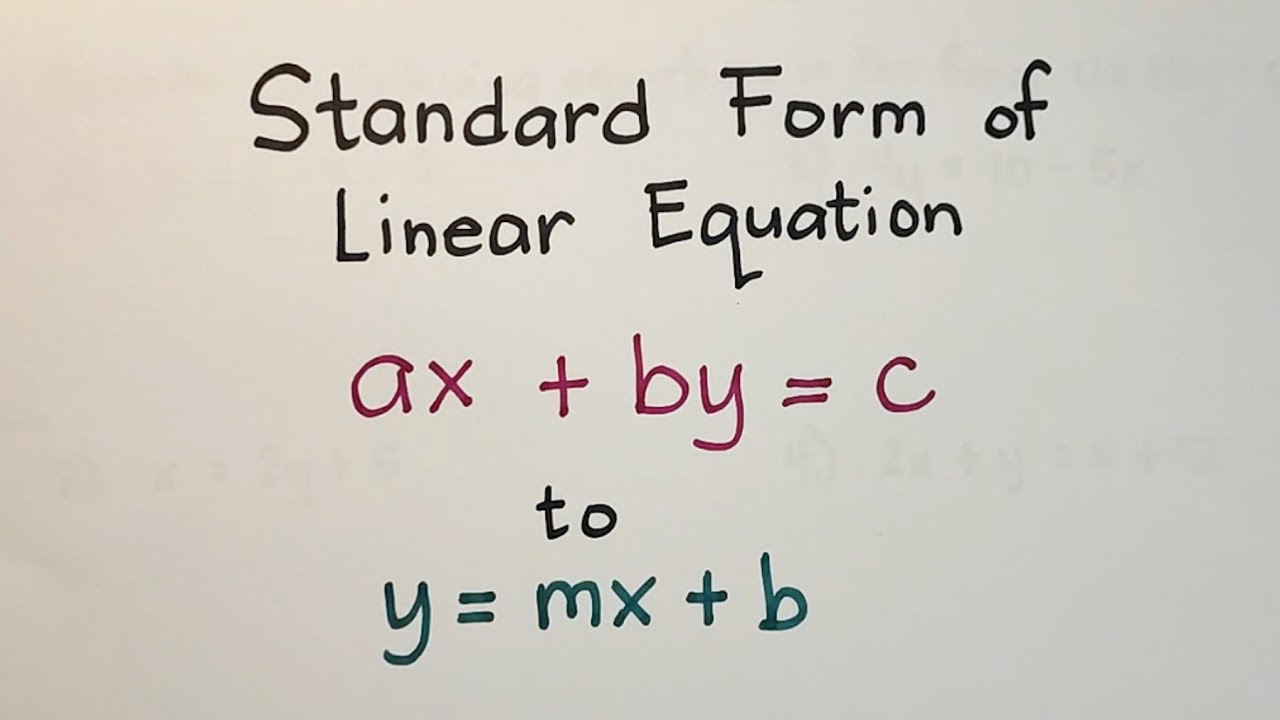

Detail Author:
- Name : Citlalli Harvey
- Username : roslyn84
- Email : jay07@hotmail.com
- Birthdate : 1988-01-12
- Address : 39862 Gardner Club New Louisaberg, CO 73499-3458
- Phone : 1-610-541-4690
- Company : Ernser and Sons
- Job : Supervisor of Police
- Bio : Deserunt itaque impedit consectetur quisquam qui. Est sint quisquam ullam voluptatem omnis autem. Molestiae voluptatum molestiae eum sint quas. Consequatur est amet mollitia id assumenda ut et.
Socials
instagram:
- url : https://instagram.com/jschamberger
- username : jschamberger
- bio : Nesciunt enim eius accusantium molestiae. Enim sed error quis quia voluptatem.
- followers : 2745
- following : 2035
tiktok:
- url : https://tiktok.com/@schamberger1974
- username : schamberger1974
- bio : Quas aut consequatur sed quibusdam molestias molestias ut.
- followers : 6685
- following : 285
twitter:
- url : https://twitter.com/julieschamberger
- username : julieschamberger
- bio : Beatae culpa et quia. Ut non aliquid iure molestias aperiam ut recusandae facere.
- followers : 2711
- following : 2289