Math Symbols Explained: Decoding Mean, And, & More!

24 May, 2025

Ever pondered the intricate dance of numbers and symbols, the very language that unlocks the secrets of the universe? Mathematics, at its core, is a language of precision, and understanding its symbols is the key to unlocking its profound truths.

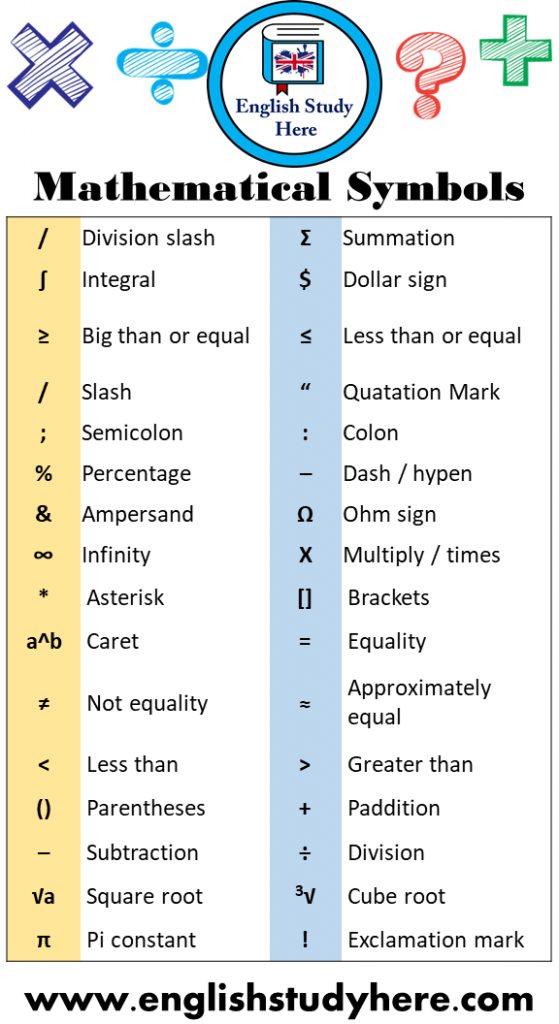
The landscape of mathematics is populated by a vast array of symbols, each with its specific role and meaning. These symbols aren't just arbitrary marks; they are the building blocks of complex ideas, allowing mathematicians to express intricate relationships and solve intricate problems. While many of these symbols are universally recognized within the mathematical community, their meanings can sometimes shift depending on the context, the branch of mathematics, or even the specific problem at hand. This article aims to demystify one of the most fundamental symbols in mathematics, exploring its definition, its implications, and its various applications.

Symbol	Meaning	Context	Examples
+	Addition/Conjunction	Arithmetic, Logic	2 + 2 = 4 (Arithmetic); A + B (Logical Conjunction)
-	Subtraction/Negation	Arithmetic, Logic	5 - 2 = 3 (Arithmetic); -A (Logical Negation)
x or	Multiplication	Arithmetic, Algebra	3 x 4 = 12 or 3 4 = 12
/	Division	Arithmetic, Algebra	10 / 2 = 5
=	Equals/Equality	All Branches	2 + 2 = 4
	Not Equal To	All Branches	5 2
<	Less Than	Inequalities	2 < 5
>	Greater Than	Inequalities	7 > 3
	Less Than or Equal To	Inequalities	x 5
	Greater Than or Equal To	Inequalities	x 10
	Square Root	Algebra, Calculus	9 = 3
%	Percent	Arithmetic, Statistics	25% = 25/100
	Summation	Calculus, Statistics	from i=1 to 5 of i = 1 + 2 + 3 + 4 + 5 = 15
	Integral	Calculus	x dx
	Infinity	Calculus, Set Theory	The set of all real numbers extends to infinity.
	Union	Set Theory	A B represents the set containing all elements of A and B.
	Intersection	Set Theory	A B represents the set containing elements common to both A and B.
	Therefore	Proofs, Logical Arguments	Given A and B, C
	Element of	Set Theory	1 {1, 2, 3}
	Not an element of	Set Theory	4 {1, 2, 3}

The symbol "+", often associated with addition in basic arithmetic, also plays a crucial role in mathematical logic. While in elementary math, the plus sign is a straightforward indicator of the operation of adding two quantities together, in probability and logic, it serves as the symbol for the logical conjunction "and." To fully grasp this dual role, let's begin by exploring the symbol's use in basic arithmetic.

In the realm of arithmetic, the "+" symbol performs a simple, yet fundamental task: it signifies addition. For instance, when we see "2 + 2 = 4," we immediately understand that we are combining two quantities to find their total. This concept of combining quantities extends to more complex operations and is the foundation of nearly all mathematical calculations. The plus sign is an operator, telling us to combine these numbers, whatever they are, in a specific way. Without the plus sign, we would not know what calculation to perform. So, in its simplest form, the plus sign tells us to add.

The meaning of "+" in logic may not be so easy to grasp, but the function remains. The logical conjunction, symbolized by "+", indicates that two conditions must both be true for the overall statement to be considered true. Think of it as a mathematical equivalent of the word "and." If we say "A + B," this means that both statement A and statement B must be true for the combined statement to be true. It's essential to differentiate this from the arithmetic sense, where the result is a single numerical value.

In probability, the distinction becomes clearer. Consider the concept of independent events. If event A has a probability of happening and event B has a probability of happening, then the probability of both events occurring ("A and B") is calculated by multiplying the probabilities of the two individual events. The "and" here represents the combined probability of both events, just as the plus sign in mathematics combines quantities.

This duality illustrates a critical point about mathematical symbols: their meanings are often context-dependent. A single symbol can represent different operations or concepts depending on the branch of mathematics in which it is used, or even the specific formula where it appears. This flexibility allows mathematicians to express a wide variety of concepts in a precise and concise manner. Recognizing the specific meaning of a symbol requires understanding the context in which it is presented. This is why the study of mathematics involves not only learning formulas and calculations but also developing an understanding of mathematical language.

Let's delve into the concept of "mean" in the context of statistics, a field where mathematical symbols, including "+" and others, find extensive application. The mean, often interchangeably referred to as the average, provides a single value that summarizes an entire dataset. The mean represents the central point or a typical value within a dataset. To calculate the mean, the values of a set are summed and then divided by the total number of values in that set. This fundamental statistical measure offers insights into the characteristics of the data under study. For instance, if we wish to find the mean of the numbers 2, 7, and 9, we would first add them together (2 + 7 + 9 = 18) and then divide the sum by the number of elements (18 / 3 = 6). Thus, the mean of the numbers 2, 7, and 9 is 6. This value serves as a representative figure for the dataset as a whole.

However, the arithmetic mean is not the sole type of mean. Other variations exist, such as the geometric mean and the harmonic mean, which are used in different contexts. The geometric mean is often used when dealing with rates of change, whereas the harmonic mean is useful in situations involving rates or ratios. The "and" operator comes into play in such contexts when calculating the mean across several data points.

Consider the statement: "25% means 25 per 100." This statement illustrates the use of percentage which helps in converting fractions, and helps in understanding of the ratio of a number over a hundred. This simple concept is used across many areas and is especially useful when comparing different sets of data. The concept is further developed with the concept of central tendency, which is critical for understanding data. This includes the concepts of mean, median, and mode. The arithmetic mean, which we have already addressed, is one of the most commonly used measures of central tendency.

Mathematics is the subject that employs numbers, shapes, and space. The study of mathematics helps us gain knowledge. Learning mathematics helps students grow. The use of mathematical symbols is critical to the understanding of mathematics. These symbols refer to quantities and illustrate the relationship between two quantities. In mathematics, the use of symbols is central to the performance of mathematical operations.

The versatility of math symbols is particularly evident in how they represent relationships. Take, for example, the concept of inequalities. The "<" symbol (less than) and the ">" symbol (greater than) clearly define the relationship between two numbers. If we say "2 < 5," we instantly understand that 2 is less than 5. Similarly, "7 > 3" tells us that 7 is greater than 3. There are other inequality signs that help us define the data even further.

The power of mathematical notation lies in its ability to encapsulate complex ideas concisely. It transforms lengthy descriptions into a shorthand language. We can combine them like this: "0 < s < l < 10," which means 0 is less than the short length, and the short length is less than the long length, and the long length is less than 10. This is a simple yet effective use of symbols.

Understanding the symbols of mathematics, from the simple ones like "+" and "-" to more complex ones like "" (integral) and "" (summation), is fundamental to navigating the subject. Each symbol carries specific meaning and allows us to perform precise operations. This glossary is a resource designed to provide explanations of mathematical terms and concepts. It serves as a guide to mathematical language.

Mathematics serves as the language of science and the universe. It is integral to academic disciplines and has a role in real-life situations. The ability to understand mathematical symbols is essential for comprehending science. These symbols facilitate precise expressions of scientific principles.

32+ Mathematical Symbols And Their Meanings That You Should Know

Details

Details

32 Mathematical Symbols & Signs and Meanings English Study Here

Details

Detail Author:

Name : Miss Herminia Doyle V
Username : brady89
Email : cgoyette@gmail.com
Birthdate : 2000-06-17
Address : 364 Cedrick Isle Suite 487 Abernathyhaven, NJ 30426-6162
Phone : 458-995-4189
Company : Bayer and Sons
Job : Pipe Fitter
Bio : Velit amet voluptas sint voluptatum sunt debitis est. Aperiam impedit et sint. Ea alias autem aspernatur sint tempore.

Socials

linkedin:

url : https://linkedin.com/in/karina_oberbrunner
username : karina_oberbrunner
bio : Aut est culpa qui sequi aut et unde consequatur.
followers : 1651
following : 1440

twitter:

url : https://twitter.com/karina.oberbrunner
username : karina.oberbrunner
bio : Aliquam qui laudantium est vitae consequatur maiores eius. Inventore nam quia architecto. Dolor sunt magni sed aperiam nostrum ipsam.
followers : 6726
following : 1583