Learn Graphing Functions Easily With Online Tools & Examples

24 May, 2025

Can the complex world of mathematics truly be demystified and visualized with ease? The answer lies in the power of graphing, a fundamental tool that transforms abstract equations into tangible, understandable forms.

The allure of mathematics often lies in its ability to describe and predict the world around us. From the flight of a bird to the trajectory of a rocket, mathematical functions hold the keys to understanding these phenomena. But how do we bridge the gap between the abstract symbols of equations and the concrete realities they represent? The answer, in many cases, is the graph.

At its heart, a graph is a visual representation of a function. A function, in the mathematical sense, is a relationship between two sets of numbers: the domain (the input values) and the codomain (the output values). The graph provides a visual map of this relationship, allowing us to see how the output changes as the input varies. A function can be represented in various ways, including equations, tables, and verbal descriptions, but the graph is often the most intuitive. It allows us to "see" the function's behavior at a glance, identifying key features like its increasing or decreasing intervals, its maxima and minima, and its symmetry properties.

Consider the simple linear function, like y = 2x + 1. This equation represents a straight line when graphed. Every point on that line represents a valid (x, y) pair that satisfies the equation. For every input 'x', the equation provides a corresponding output 'y', and when plotted on a coordinate plane, these (x, y) pairs create the line. Understanding this fundamental concept forms the building block for exploring more complex mathematical ideas. When we represent an equation or formula as a graph, we adjust our definition of the graph somewhat, defining each point as an (x,y) pair that satisfies that function's equation.

A function can undergo a variety of transformations, altering its appearance on a graph. One of the most basic is translation, where the entire graph is shifted up, down, left, or right. For example, the function f(x) + c shifts the graph of f(x) c units upwards. Conversely, f(x) - c shifts it downwards. Similarly, f(x + c) shifts it to the left, and f(x - c) shifts it to the right. Another type is dilation, the graph gets stretched or compressed horizontally or vertically. In horizontal dilation, f(ax) compresses or stretches the graph by a factor of 1/a. And of course, reflection flips the graph across an axis. These transformations not only give insight into the relationship of equations and their graphs, they allow for a deeper understanding of functions.

When dealing with functions, the vertical line test is a useful tool. This test states that a graph is a function if no vertical line intersects the graph at more than one point. If a vertical line crosses the graph at multiple locations, it indicates that for a single x-value, there are multiple corresponding y-values, which violates the definition of a function. Conversely, if any horizontal line drawn on the graph intersects the curve more than once, it indicates the function is not one-to-one. This test is invaluable when analyzing whether a graph truly represents a function.

Let's apply this to an example: Is a circle on a graph a function? A circle fails the vertical line test. Any vertical line drawn through the circle (except the extreme tangent lines) will intersect the circle at two points. Therefore, a circle is not a function.

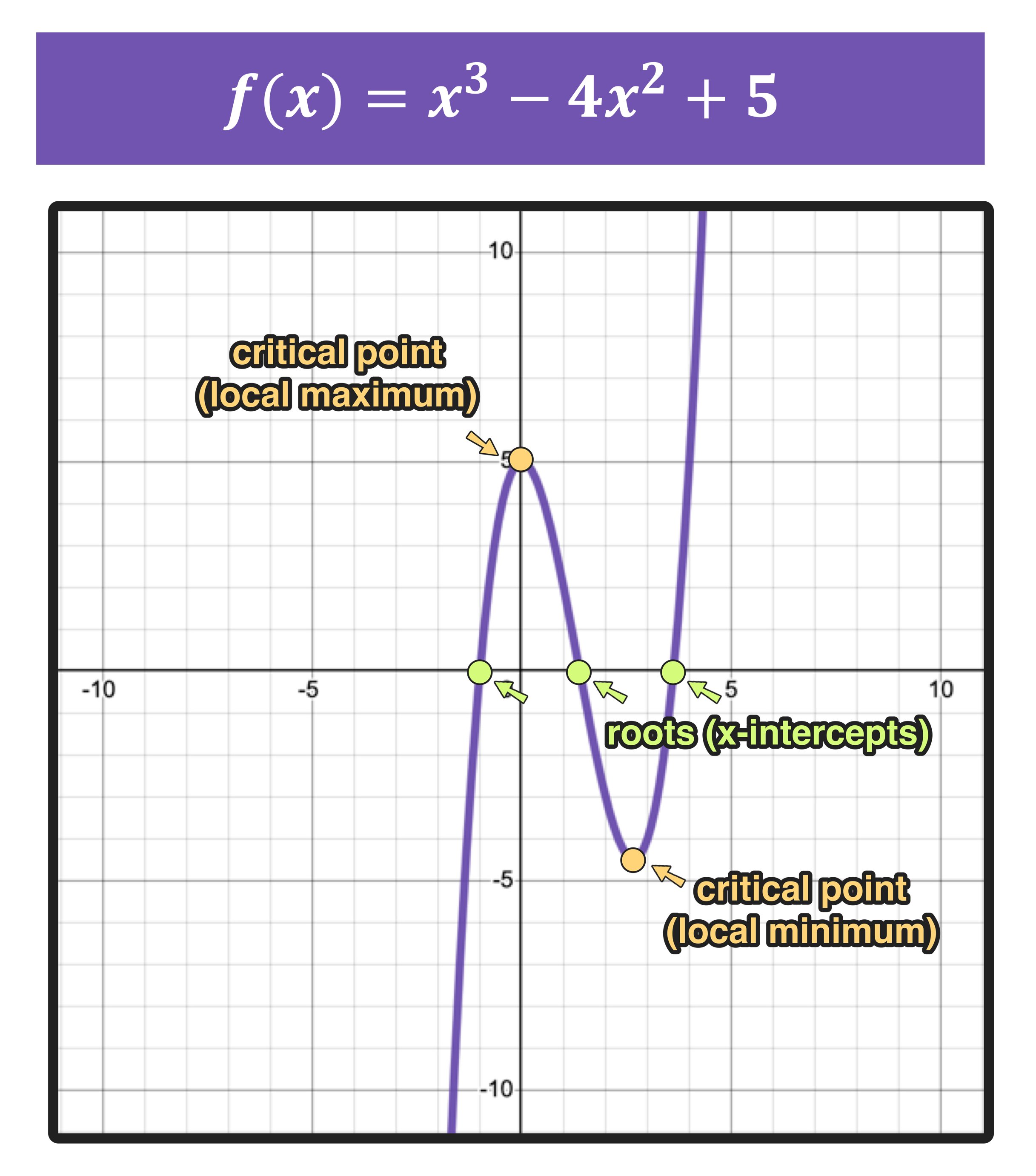
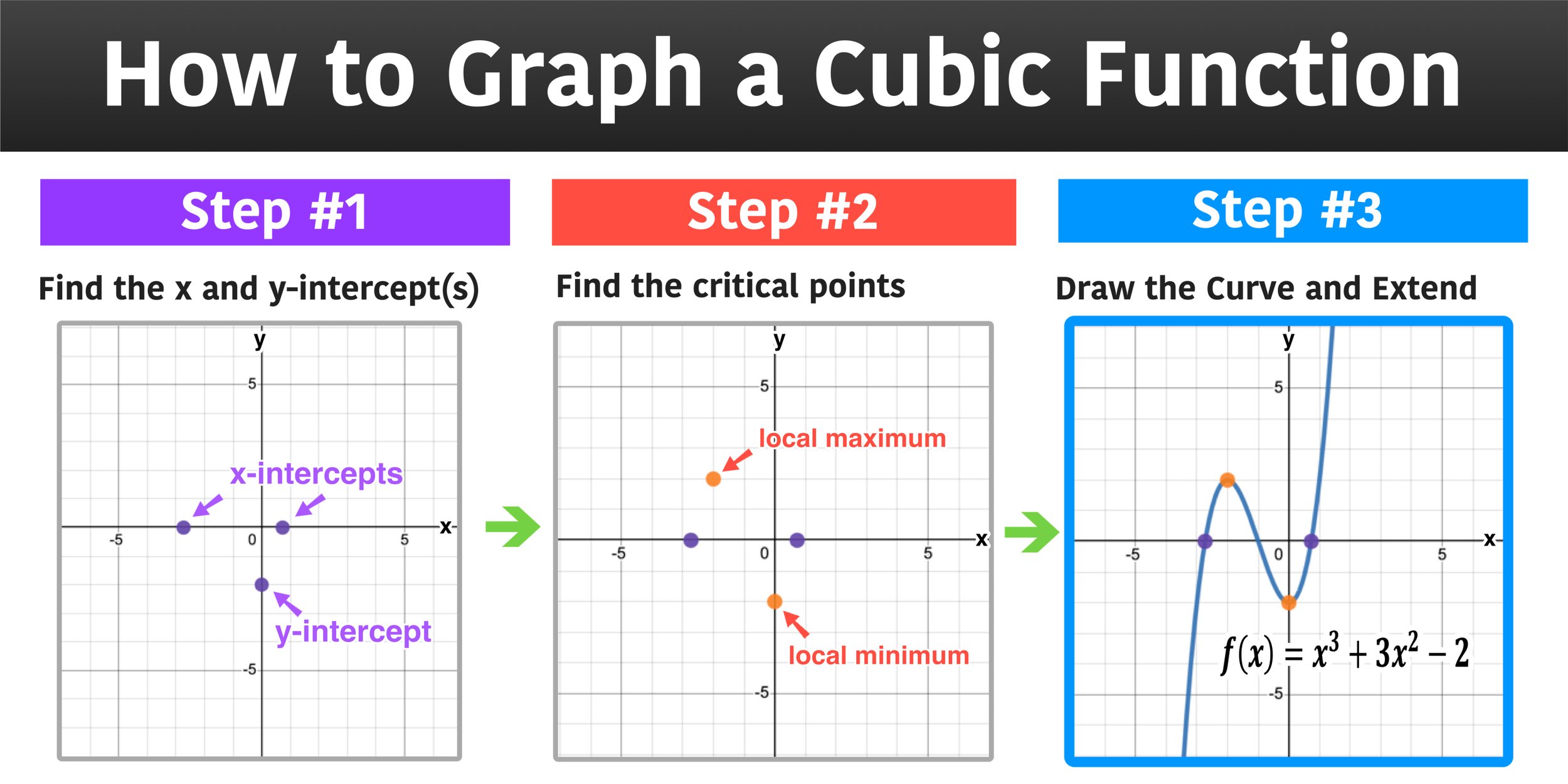
Graphing functions can be simplified when following certain guidelines. Begin by determining the domain and range of the function. Then, look for any symmetry properties, which can help simplify the graphing process. Find the x and y intercepts. Test for asymptotes, then plot additional points. Finally, draw the curve, making sure that the functions key characteristics, such as increasing or decreasing intervals, and the presence of any asymptotes, are correctly reflected in the graph.

We now have enough analytical tools to draw graphs of a wide variety of algebraic and transcendental functions. For example, when graphing a rational function like f(x) = 1/x, it is important to recognize the presence of asymptotes. To grasp the relationship between functions, consider graphing multiple functions on the same axes. For instance, if we graph f(x) and g(x) = f(x) + 2 on the same axes, we can readily see that g(x) is f(x) shifted upwards by two units. This approach provides insight into how functions interact with each other. The first function, f(x), can be found to be increasing over its entire domain. Graphing multiple functions on the same axes provides greater insight into their relationship.

Another way to analyze and graph a function is through function transformation. Function transformations refer to how the graphs of functions move, resize, or reflect according to the equation of the function. By understanding these, graphing a function becomes far simpler. Transforming a function allows for its equation to be translated by a shift up, down, left, or right. They also allow for reflection, stretch, or compression. Graphing a linear function is, in itself, an application of these transformation techniques. It can be accomplished by using transformations on the identity function f(x) = x.

The derivative function plays a critical role in understanding the behavior of a function. The derivative of a function, f'(x), measures its instantaneous rate of change. The value of the derivative at a point on the original function's graph represents the slope of the tangent line at that point. Graphing the derivative function from the graph of a given function helps to visually represent its rate of change. The derivative function can also reveal the critical points of a function where the function changes direction, or where the function's rate of change is zero. There are also conditions for when a function does not have a derivative. A function does not have a derivative at a point where its graph has a sharp corner or a cusp, where it has a vertical tangent, or where the function is discontinuous.

Concept	Description
Function	A relationship between a set of inputs (domain) and a set of outputs (codomain), where each input has exactly one output.
Graph of a Function	A visual representation of a function, plotted on a coordinate plane, showing the relationship between input and output values.
Domain	The set of all possible input values for a function.
Codomain	The set of all possible output values for a function.
Vertical Line Test	A method to determine if a graph represents a function. If any vertical line intersects the graph at more than one point, the graph does not represent a function.
Function Transformations	Changes made to a function that alter its graph, including translations, dilations, and reflections.
Translation	Shifting the graph of a function up, down, left, or right.
Dilation	Stretching or compressing the graph of a function horizontally or vertically.
Reflection	Flipping the graph of a function across an axis.
Derivative Function	A function that represents the instantaneous rate of change of another function.
Continuity	A function is continuous at a point if there are no abrupt changes or breaks in the graph at that point.
Asymptote	A line that a curve approaches but never touches as it tends towards infinity.

In conclusion, the power of graphing functions lies in its ability to transform abstract concepts into visual realities. By using graphing, we can study equations, examine the properties of functions, and apply these concepts to solve problems. The ability to graph functions is an essential skill for anyone studying math, science, or engineering, providing a vital tool for understanding and interacting with the world around us.

How to Graph a Function in 3 Easy Steps — Mashup Math

Details

How to Graph a Rational Function 8 Steps (with Pictures)

Details

Detail Author:

Name : Osbaldo Aufderhar V
Username : borer.trace
Email : pmurray@braun.org
Birthdate : 1980-05-10
Address : 2574 Jalon Loop Littleview, AR 57111-1905
Phone : +1-689-396-0057
Company : McCullough-Schaden
Job : Visual Designer
Bio : Rerum quia est expedita voluptatem veritatis. Perspiciatis ducimus odio repudiandae possimus architecto. Enim unde fugit non id.

Socials

facebook:

url : https://facebook.com/runolfsson1972
username : runolfsson1972
bio : Harum alias rerum aspernatur ipsum velit sequi.
followers : 731
following : 958

linkedin:

url : https://linkedin.com/in/jarrett.runolfsson
username : jarrett.runolfsson
bio : Aliquam doloremque est animi voluptas.
followers : 4916
following : 2882

twitter:

url : https://twitter.com/jarrett_runolfsson
username : jarrett_runolfsson
bio : Sed cumque cumque iusto velit aut ullam. Debitis aut esse minima molestiae. Quia id qui quo ipsa quasi.
followers : 3171
following : 2239